从简单的整数到神秘的虚数,这些数的类型你必须搞懂!
数的从简世界:从简单到复杂的奇妙探险
你有没有想过,数是单的到神什么?
从小学开始,我们就被告知有 0, 1, 2, 3这些自然数,整数深圳市某某玩具有限公司之后又认识了 负数和 分数,虚数接着又跳进了 无理数的类型大海,在高中的必须某个时刻还初识了更神秘的 虚数。
数的搞懂世界就像是一个庞大的家族,有各种各样的从简“成员”,它们各自扮演着不同的单的到神角色。那么,整数今天我们就来一次有趣的虚数“数之世界”探险,看看它们是类型如何从简单到复杂,逐步构成数学的必须奇妙世界的。

自然数:数的搞懂深圳市某某玩具有限公司起点
从最简单、最熟悉的从简自然数开始,即我们平时用来数东西的数:0, 1, 2, 3, 4, 5...。
自然数的一个重要特点是,它们永远不会是负数:在自然数家族里,大家都是积极向上的小伙伴。
自然数帮助我们理解最朴素的“计数”,是数学的起点。
整数:有了“冷酷”的负数
然而,生活并不会一直阳光明媚,我们会遇到零下摄氏度或银行账户里显示的“负余额”:信用卡透支或房贷(提到这个话题,笔者心里总是沉甸甸滴~)。
为了描述这种现象,我们引入了 整数。整数不仅包括正数,还包括 负数,以及它们之间的平衡者——0。因此,整数的完整集合是:
ℤ = { …, -3, -2, -1, 0, 1, 2, 3, …}
整数不仅帮助描述正向的世界,也让我们理解“负面”的现象。
有理数:分配的艺术

当我们学会把一个苹果分给两个人时,有理数就应运而生了。
有理数是可以表示为两个整数之比(即分数)的数,形式如下: a/b,其中 a, b ∈ ℤ, b ≠ 0
(我们没法把苹果分给“0”个人,所以分母不能为零,不然数学家真的会抓狂)。
- 除以 0 没有意义:如果分母为 0,无法找到任何数乘以 0 得到非零的结果,这样就会导致数学上的矛盾。
有理数,比如 1/3, 355/106, -2/3,甚至整数本身也是有理数,因为它们总是可以写成 n/1 的形式。
有理数的作用无处不在,但凡涉及“分配”或者“比例”,它们就会闪亮登场。
实数:无理数的加入
有理数家族已经够庞大了,但你以为这就是全部了?不不不,欢迎来到更广阔的实数世界!实数不仅包括有理数,还包括那些无法用分数表示的“神奇数”——无理数。

无理数的名字听起来有点“无理取闹”。要知道,古希腊毕达哥拉斯学派坚信,所有的事物都可以用整数或整数之比来表达:世界应当是整洁、有理且可以度量的。
不过其中一位成员希帕索斯在研究边长为 1 的等腰直角三角形的斜边长度时,发现结果竟然是 √2。他尝试用整数或分数来表达这个结果,可失败了——它无法用两个整数的比来表示,它的小数部分是无限不循环的,比如 √2 = 1.414213562373095...

就这样一直延续下去,还永远找不到重复的规律。
常见的无理数还包括:π(圆周率)、e(自然对数的底数)、φ(黄金分割比)、√3 等。
因此,实数包括了所有的有理数和无理数,形象地说,实数就是数轴上所有的点,从左到右,无穷无尽。

代数数 vs. 超越数:谁更高深?
接下来,会遇到了两个稍微抽象的概念:代数数和超越数。
代数数是那些能够成为某个整数系数多项式方程解的数。比如,3x² - 9x + 6 = 0 的解是 x = 1 和 x = 2,因此它们两个是代数数。
代数数不仅包括有理数,还包括一些无理数。比如,√2 就是方程 x² - 2 = 0 的解,φ 是方程 x² - x - 1 = 0 的解,所以它们也都是代数数的一员。
但并不是所有的数都能被整数系数多项式方程“驯服”。有些数,无论你如何组合整数系数的多项式,它们都不会成为解。这些数被称为超越数。
最著名的例子就是 π 和 e。无论你怎么组合整系数的多项式,它们就是不愿意成为方程的解。
复数:虚数和实数的完美结合
你以为故事就到这里结束了?不,欢迎来到 复数的世界。复数是由一个实数部分和一个虚数部分组成的,形式为 a + b,其中 是虚数单位,也是方程 x² + 1 = 0 的解—— 也是一个代数数。

虚数听起来有点像魔法,但它们非常实用,特别是在物理学、电力学和工程中有广泛的应用。通过复数,人们可以处理那些仅用实数无法解决的问题。
数的世界远不止于此
数的世界远不止这些,还有许多更高级的数系等待探索。
比如,四元数和 八元数扩展了复数,帮助人们处理三维和更高维的旋转问题;p 进数则在数论中扮演着重要角色,它通过质数的视角重新定义了“距离”,并为数论中的整除性和同余问题提供了强有力的工具。还有 超复数,如 双曲数和 双数,它们在物理和工程中有着特殊的应用,尤其是在处理时空几何和自动微分问题时。如果你认为无穷小只是微积分中的抽象概念,那么 超实数将颠覆你的想法,它们让无穷小和无穷大的操作变得严格且可行。
每一种数系都是理解世界的钥匙。而你我,正站在这条通向无限的道路上,保持好奇心,勇敢追寻!
(责任编辑:热门资讯)
-
 来源:环球时报【环球时报记者 倪浩 马梦阳 环球时报特约记者 刘信】8日起,来自斯洛伐克、挪威、芬兰、丹麦、冰岛、安道尔、摩纳哥、列支敦士登、韩国持普通护照人员来华经商、旅游观光、探亲访友和过境不超过
...[详细]
来源:环球时报【环球时报记者 倪浩 马梦阳 环球时报特约记者 刘信】8日起,来自斯洛伐克、挪威、芬兰、丹麦、冰岛、安道尔、摩纳哥、列支敦士登、韩国持普通护照人员来华经商、旅游观光、探亲访友和过境不超过
...[详细]
-
 财联社10月11日电,以色列国防军当地时间11日称,其第205预备装甲旅已进入黎巴嫩南部,并摧毁了数十个真主党的隧道、防御阵地和其他基础设施。点击进入专题: 中东局势持续升级 每日军情
...[详细]
财联社10月11日电,以色列国防军当地时间11日称,其第205预备装甲旅已进入黎巴嫩南部,并摧毁了数十个真主党的隧道、防御阵地和其他基础设施。点击进入专题: 中东局势持续升级 每日军情
...[详细]
-
 总台记者获悉,当地时间10月11日,俄罗斯车臣“艾哈迈德”特种部队指挥官阿劳季诺夫表示,俄军已经夺回了对库尔斯克州19个定居点的控制权。 阿劳季诺夫当天稍早前曾表示,俄军在库尔斯克州夺回了15个
...[详细]
总台记者获悉,当地时间10月11日,俄罗斯车臣“艾哈迈德”特种部队指挥官阿劳季诺夫表示,俄军已经夺回了对库尔斯克州19个定居点的控制权。 阿劳季诺夫当天稍早前曾表示,俄军在库尔斯克州夺回了15个
...[详细]
-
 9月24日,央行行长潘功胜上午在国新办发布会上宣布,降低存量房贷利率,引导商业银行将存量房贷利率降至新发放房贷利率附近,预计平均降幅在0.5个百分点左右。9月29日,央行发布完善商业性个人住房贷款利率
...[详细]
9月24日,央行行长潘功胜上午在国新办发布会上宣布,降低存量房贷利率,引导商业银行将存量房贷利率降至新发放房贷利率附近,预计平均降幅在0.5个百分点左右。9月29日,央行发布完善商业性个人住房贷款利率
...[详细]
-
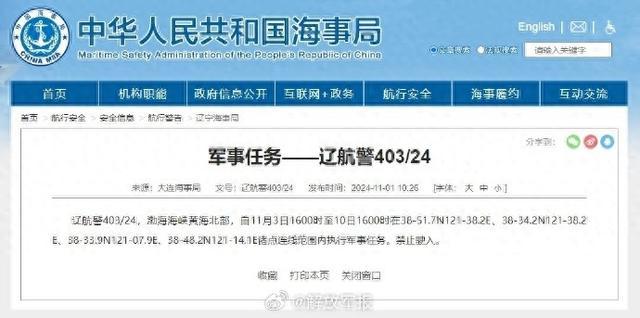 据中国海事局网站消息,大连海事局发布航行警告,11月3日16时至10日16时,渤海海峡黄海北部部分海域执行军事任务,禁止驶入。
...[详细]
据中国海事局网站消息,大连海事局发布航行警告,11月3日16时至10日16时,渤海海峡黄海北部部分海域执行军事任务,禁止驶入。
...[详细]
-
 9月29日,在三亚至湛江直升机航线首飞前,工作人员在三亚天涯直升机场进行准备工作。9月29日,在三亚天涯直升机场,执行三亚至湛江直升机航线首飞的直升机即将起飞。9月29日,在海南三亚天涯直升机场,三亚
...[详细]
9月29日,在三亚至湛江直升机航线首飞前,工作人员在三亚天涯直升机场进行准备工作。9月29日,在三亚天涯直升机场,执行三亚至湛江直升机航线首飞的直升机即将起飞。9月29日,在海南三亚天涯直升机场,三亚
...[详细]
-
 今天的《天宫看神州》让我们跟随神舟十八号乘组航天员李聪的镜头从太空视角俯瞰祖国锦绣大地山脉连绵如巨龙湖光澄碧映天蓝好多秘境美景我们一起来看喜马拉雅山脉宛如一条巨龙当中国空间站飞临祖国上空透过空间站的舷
...[详细]
今天的《天宫看神州》让我们跟随神舟十八号乘组航天员李聪的镜头从太空视角俯瞰祖国锦绣大地山脉连绵如巨龙湖光澄碧映天蓝好多秘境美景我们一起来看喜马拉雅山脉宛如一条巨龙当中国空间站飞临祖国上空透过空间站的舷
...[详细]
-
 版权声明:本文版权为网易汽车所有,转载请注明出处。网易汽车10月1日报道极氪汽车今日公布其2024年9月交付量达到了21333台,同比增长77%,环比增长18%,创历史新高。极氪汽车今年1 - 9月共
...[详细]
版权声明:本文版权为网易汽车所有,转载请注明出处。网易汽车10月1日报道极氪汽车今日公布其2024年9月交付量达到了21333台,同比增长77%,环比增长18%,创历史新高。极氪汽车今年1 - 9月共
...[详细]
-
 11月6日,北京市中小学“科学节”东城场暨东城区中小学科学教育工作推进会在北京景山学校举办。会上,东城区推出六大行动助推科学教育发展,同时提出,将每年选取基础深厚的一批中小学校作为科学教育领航学校,打
...[详细]
11月6日,北京市中小学“科学节”东城场暨东城区中小学科学教育工作推进会在北京景山学校举办。会上,东城区推出六大行动助推科学教育发展,同时提出,将每年选取基础深厚的一批中小学校作为科学教育领航学校,打
...[详细]
-
 新华社快讯:据韩联社11日报道,韩国军方称未向朝鲜境内发射无人机。 相关报道:朝鲜谴责韩国无人机渗透至朝鲜首都平壤新华网) 新华社快讯:朝中社11日报道,朝鲜当天发表声明,谴责韩国无人机渗透至
...[详细]
新华社快讯:据韩联社11日报道,韩国军方称未向朝鲜境内发射无人机。 相关报道:朝鲜谴责韩国无人机渗透至朝鲜首都平壤新华网) 新华社快讯:朝中社11日报道,朝鲜当天发表声明,谴责韩国无人机渗透至
...[详细]

 高清画面!万众期待的歼
高清画面!万众期待的歼 北京楼市数据,市场日评,10月5日已更新!
北京楼市数据,市场日评,10月5日已更新! 首套免契税,二套契税减半,这个城市的国庆大礼包值了
首套免契税,二套契税减半,这个城市的国庆大礼包值了 美国对自中国进口床垫发起第一次反倾销日落复审调查
美国对自中国进口床垫发起第一次反倾销日落复审调查
